I’ve had almost two weeks to think about the impact of Wolfram|Alpha (abbreviated as W|A, and now pronounced by me as “Walpha”), and I’m ready to share some of my thoughts with you.
After spending hundreds of hours reading more than 200 papers on innovation in math instructional practices, change in higher education, and diffusion of innovation theory, it is strange to suddenly find myself observing the possibility of a sudden shift in math education caused by a new innovation. I liken it to being a vulcanologist who has, up until this point, been observing a dormant volcano and then quite unexpectedly, it begins rumbling.

Please keep in mind that these are my own predictions and thoughts, for better or for worse.
1. The adoption rate of W|A amongst students in higher education will be extremely fast.
I’ve examined the attributes and variables that affect the diffusion of innovations, and found that every single one points to a fast adoption amongst students. Because W|A is free and similar to other technologies they know how to use (designed like a search engine), it has relative advantage over other CAS technologies. With prior CAS technologies, you had to know exactly what series of steps or commands to write in order to extract the outcome you desired, but with W|A, the less you ask for, the more you get out. W|A just assumes you want all relevant information it can generate. W|A is easily trialable – anyone with Internet access can try it. Not only that, but observability is also high – simply use a hyperlink to share what you’re doing in W|A with others. Compound this ease of observability with the incredible connectedness of the student population in the U.S. (Facebook, MySpace, etc.), and you can see why I don’t think it will take long for W|A to spread to the undergraduate population of math students.
Most students take their math classes for one reason: they are required to for their degree. W|A will provide solutions to problems, relevant mathematical information, and in many cases, steps for how the solution was obtained. Thus, for the reason that it appears to be a means to an end (getting through that math course with the least pain possible), using W|A to help complete assignments for math courses will be extremely compatible with the belief systems of these students.
2. There will be a sizable group of math instructors that immediately shifts to using Wolfram Alpha in instruction, and thus, begins to shift the curriculum in those classes away from computational mathematics.
I’ve already outlined many reasons why students will be fast adopters, and for the most part, these are the same reasons that instructors will be fast adopters (high relative advantage, low complexity, good trialability and observability). The main difference between the student and instructor populations will be the compatibility between their beliefs systems and the innovation. This is the only attribute where the adoption rate of W|A might be slowed. For example, Computer Algebra System (CAS) technology (TI-89 calculators, Maple, Mathematica, etc.) has been around for at least 10 years, and yet CAS is not widely adopted in math courses (see the latest CBMS Statistical Report).
That’s not to say that math instructor beliefs aren’t compatible with the use of CAS Technologies. I suspect that many, like myself, simply found that implementation of CAS in the classroom was too difficult. In my case, I questioned how could I ask my students, who already had a non CAS-calculator in-hand from high school, to pay for extra software or another calculator to adopt the curriculum to CAS-inclusion. To teach using software (before students all began buying laptops), we would require computer labs and site licensing, and this was not in the budget for many of us. Whether it was calculators or software, either decision would require students to spend more money, and thus, these were decisions that would likely have required department buy-in.
What does this mean for the adoption of W|A today? Instructors who already teach with CAS technologies will easily make the shift to using W|A. Instructors who liked the idea of teaching with CAS, but were unable to implement for logistical reasons, will quickly also quickly make the shift to using W|A (you may think I’m full of it here, but I already know of several who have already changed their courses). The real beauty of W|A being free is that individual instructors, under the umbrella of academic freedom, do not have to ask their departments or colleagues for buy-in. Shoud they? Yes. And if they are under some kind of contract to teach in a prescribed manner given by the department, then they should definitely ask. But for the majority of us, if we just decided to change our courses tomorrow, very little could be done to stop it.
For my complete analysis of the rate of diffusion of W|A, you can download the 2-page analysis or view the slides that compare CAS and W|A.
3. There will be a sizable group of math instructors that attempt to either ignore W|A or put up an active resistance to it.
While some instructors will actively ignore the existence of W|A (look at the theory of cognitive dissonance), some will just passively miss it for a while (you know, by ignoring that email that they get sent that warns them to take a look at what W|A does).
However, given that there are still pockets of instructors and departments in the U.S. where graphing calculators are still not allowed, some instructors will likely react with resistance (i.e. we still don’t change anything) or possibly even with the charge that using W|A is cheating. For these instructors, compatibility of beliefs is not there.
4. We can change if we do so by focusing on areas of agreement instead of disagreement.
Mathematicians in higher education have been divided over reform teaching for 20 years now. Much like some of the political hot potatoes of our time (which shall go unnamed here for fear of blog spammers), it is unlikely that the two camps of traditionalists and reformists will ever sway followers from the opposite side. However, we can hope to agree on a middle ground. I think we would all agree that we want to make sure that math instruction focuses on learning concepts. I think we would all agree that some understanding of algebraic manipulation is important to lay the foundational structure upon which the rest of mathematical understanding is laid. I think we would all agree that there is some set of fundamental skills that must be learned extremely well in order to progress to higher levels of mathematics. Finally, I think we would all unanimously agree that we wish we had more time in our classes to be flexible in what we teach – to bring in interesting mathematical examples from the world around us even if the math doesn’t directly relate to the topic of the day’s lesson.
Perhaps this is the time for us to reach out and embrace a tool that might allow us to jettison some of the computational knowledge from the curriculum, and give math instructors greater flexibility in supplemental topics in the classroom. Just like each English instructor has their own favorite books to teach with, math instructors have their own favorite topics they wish they could share with students: fractals, trend analysis, network theory, number theory, modern algebra … maybe these finally get a turn at the table.
One more thing. You (my readers) have to understand how scary this whole thing might be for some math instructors. I still think that anyone who is not a little scared by the changes that W|A brings hasn’t thought about it enough yet. I’ve always been an instructor that lived for change, and I’ve been uneasy since W|A launched on May 15. I have no doubt that I can change my courses to adapt to the new environment, and I know that in the end, the changes will be good ones – but the thought of changing so much across the board in all my courses is a daunting one.
We math folks were attracted to mathematics for its beauty, its power, and its logic. In the classroom, we have always been the beneficiaries of its non-changing nature. Algebra is algebra and calculus is calculus. In all the languages of the world, algebra and calculus have been fundamentally the same for hundreds of years. You can walk into any colleague’s class and cover for them as long as they tell you which topic to launch into. This has been a fairly easy world for us to inhabit and teach in up to now. So now, things change. And probably, they change quickly.
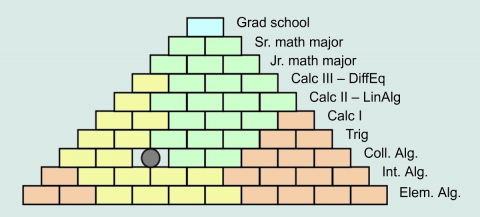
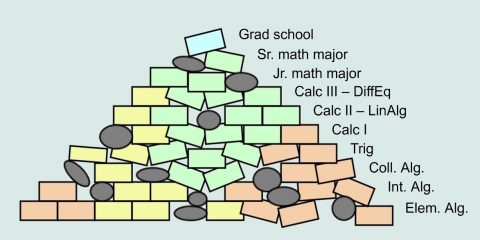
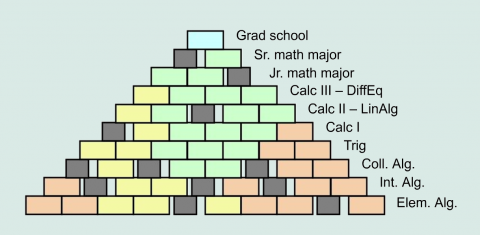
5. We all need to keep the system in mind.
None of us teaches in a vacuum. You cannot make major changes to your course without at least considering the impact that it will have when those students move to the next course, the next instructor, or the next college. Make sure that your course changes still provide sufficient “math backbone” to span students successfully to the next level of mathematics. For more on this, view the slides starting on slide #13.
Personally, I do plan to change my courses to incorporate W|A in the fall, and let me tell you that I’m grateful to have another couple of months to think about exactly how to do it. To those of you who are already using W|A this summer – you are the pioneers! Please blog, write, comment, or email about how it is going and advice for making it work.
Note: Derek has also put up a WalphaWiki where we can all begin to document how W|A handles traditional math topics and the impacts this will have on our courses.



